Introduction to Multi-Armed Bandits

I've recently been applying for Ph.D. programs and had the good fortune to connect well with a potential advisor. The professor asked me to study the online decision-making course materials on their website, and since this is a new field for me, I've created this summary based on both the MAB problem tutorials available online and the official course materials. I'd like to share my learning journey with everyone.

Note: Many viewpoints come from my understanding of the course materials and tutorials. Some parts may lack rigor or even contain errors. I welcome readers to approach this with a critical eye and share any feedback via comments or direct contact (simolark318@gmail.com).

Updates:

• September 26: Revised to include more rigorous mathematical derivations and proofs, which were underemphasized in the initial version. Some details and formulas have been corrected.
• October 15: Further formula corrections and rederivations of key sections to address previous oversights.

Chapter 1: Introduction to Multi-Armed Bandit Problems

Background: Sequential Decision Making and Feedback

The Multi-armed Bandit problem is a classic problem in probability theory within the realm of reinforcement learning.

Imagine a gambler facing N slot machines without prior knowledge of their true payout rates. How should they use the results from each play to decide which machine to play next or when to stop gambling to maximize their overall returns?

We often face a common challenge: making optimal choices with limited resources under uncertainty. These decisions are typically sequential, meaning we don't make all decisions at once but rather step by step over time. Crucially, we receive feedback after each choice that can help us adjust our future strategy. A core challenge in this decision-making process is finding the balance between exploration (trying new options to gather more information) and exploitation (making the best choice based on known information).

Problem Formalization: Multi-Armed Bandit Model

In the multi-armed bandit problem, we face $K$ different arms, each representing a possible decision or action. When we select an arm, we receive a reward drawn from a probability distribution associated with that arm. However, these distributions are unknown, and we can only learn about them by trying different arms. The more we try, the more information we gain and the better choices we can make, but this also requires more resources. Thus, our goal is to find a balance between exploration and exploitation to maximize our rewards.

Formally, we can define the problem as follows:

1. Set of Arms: There are $K$ actions or arms, denoted as $\{1, 2, \ldots , K\}$
2. Reward Distribution: When arm $i$ is selected at time $t$, we receive a reward $r_t$ drawn from a fixed but unknown probability distribution $D_a$. It's typically assumed that $r_t$ is bounded, for example, within $[0, 1]$.

Algorithm Evaluation Metrics

Here we introduce the concept of regret:

Regret: The total regret at time $T$ is defined as the accumulated difference between choosing the best arm and the rewards obtained by policy $\pi$:

$ R(T) = T \times \mu^* - \sum_{t=1}^T E[r_t] $

where $\mu^*$ is the average reward of the best arm, and $E[r_t]$ is the expected reward at time $t$ following a particular policy.

Prerequisites

Hoeffding's Inequality

Let $X_1, \ldots, X_n$ be independent random variables with $X_i \in [a_i, b_i]$. Define $R_i = b_i - a_i$. Then for any $t \geq 0$:

$ P\left(|\sum_{i=1}^{n}(X_i - \mathbb{E}[X_i])| \geq t \right) \leq 2 \exp\left(-\frac{2t^2}{\sum_{i=1}^{n}R_i^2}\right) $

If we define $\delta = 2 \exp\left(-\frac{2t^2}{\sum_{i=1}^{n}R_i^2}\right)$, using $\delta$ to express $t$, we get:

$ t = \sqrt{\sum_{i=1}^{n}R_i^2 \log\left(\frac{2}{\delta}\right)} $

Yao's Principle

Yao's Principle, named after the renowned computer scientist Andrew Yao, is a concept in computer science and computational complexity theory. It's also known as the minimax principle, used for analyzing the expected performance of algorithms or strategies in scenarios involving uncertainty or randomness.

The principle can be summarized as follows:

1. Consider a scenario where one party, called the "adversary" or "nature," controls the random choices made by an algorithm or strategy, while the other party tries to optimize its performance.
2. The adversary's goal is to make the algorithm perform as poorly as possible, while the algorithm designer tries to make it perform as well as possible. This creates a game-like scenario where the algorithm designer tries to minimize the maximum expected loss, while the adversary tries to maximize it.
3. Yao's Principle involves computing the expected performance of an algorithm assuming the adversary is doing their best to thwart the algorithm's objective.
4. By analyzing this worst-case expected performance, computer scientists can understand the lower bounds of algorithm performance, leading to better understanding of algorithm behavior and performance.

Chapter 2: Classic Algorithms

Explore-then-Exploit Algorithm

The core idea of the "Explore-then-Exploit" strategy is to conduct exploration for a period of time initially, then completely switch to exploitation. This method attempts to balance exploration and exploitation by first gathering sufficient information about each action, then selecting the best action.

Basic Steps

1. Exploration Phase: In this phase, the system uniformly tries all actions to collect information about their returns.
2. Exploitation Phase: After the exploration phase ends, the system calculates the average return for each action, then consistently selects the action with the highest average return.

Example 2.1

Suppose there are three actions: A, B, C, with true average returns as follows:

• A: 0.7
• B: 0.8
• C: 0.9

Initially, we don't know these true values. To determine which action is best, we first conduct exploration. For example, we might choose each action 10 times:

• A: Average return 0.68
• B: Average return 0.82
• C: Average return 0.89

After the exploration phase, we find that action C has the highest average return, so in the exploitation phase, we continuously select action C.

Key Point: Value of N

After understanding the basic idea of the algorithm, we find that the key question lies in the value of $N$ - how do we determine a suitable $N$ that will make the algorithm perform as well as possible?

Let's define the average reward for each action $a$ as $\hat{\mu}(a)$. We want the average reward to be as close as possible to the true expected reward, meaning we want $|\hat{\mu}(a) - \mu(a)|$ to be as small as possible.

Here we define the confidence radius as:

$ \beta_N = \sqrt{\frac{2\log{T}}{N}} $

where $\delta = \frac{2}{T^4}$

Since the regret values from pulling arm $a$ are independently and identically distributed in this scenario, we can use Hoeffding's inequality to obtain:

$ P\left\{|\bar{\mu}(a)-\mu(a)| \leq \beta_N\right\} \geq 1-\frac{2}{T^{4}} $

We define a "good event" as when all estimated values $\hat{\mu}(a)$ are close to their true values $\mu(a)$:

$ \epsilon = \{ \forall a \in [k] : | \mu\hat{a} - \mu(a) | \leq \beta_N \} $

Epsilon-Greedy Algorithm

The basic idea of the Epsilon-Greedy algorithm is that at each time step, with probability $\epsilon$ (usually a small value), it randomly selects an action (exploration), or with probability $1-\epsilon$, it selects the currently known best action (exploitation).

Basic Steps

1. Random Decision: Generate a random number between 0 and 1. If this number is less than $\epsilon$, randomly select an action; otherwise, proceed with the greedy decision.
2. Greedy Decision: Select the action with the highest known average return.

Example 2.2

Suppose there are three actions: A, B, C. The true average returns are:

• A: 0.7
• B: 0.8
• C: 0.9

At a certain point, based on past choices and returns, we know:

• A: Average return 0.65
• B: Average return 0.88
• C: Average return 0.85

If we set $\epsilon=0.1$, then 90% of the time, we will select action B because it is the known best action. But in the remaining 10% of the time, we will randomly select A, B, or C.

Successive Elimination Algorithm

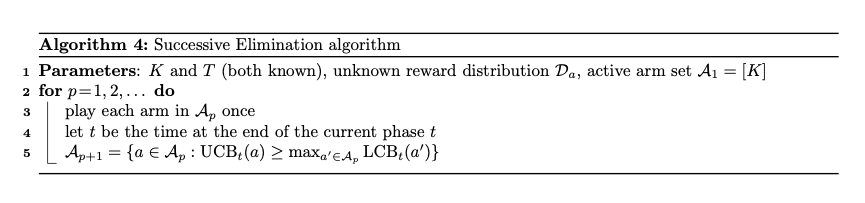
The main objective of the Successive Elimination algorithm is to minimize the required time steps to determine which action is best while reducing the selection of suboptimal actions as much as possible.

Basic Principles

1. Initialization: Each action is considered as a potentially optimal action.
2. Confidence Interval: Calculate the confidence interval for the returns of each action. For each arm $a$, the algorithm maintains a confidence interval $[LCB, UCB]$ for its reward value, where:
   • LCB (lower confidence bound): empirical mean reward $\mu\hat{t}(a) - \beta_t(a)$
   • UCB (upper confidence bound): empirical mean reward $\mu\hat{t}(a) + \beta_t(a)$
   Here $\beta_t(a)$ is the confidence interval radius that decreases as the number of pulls $N_t(a)$ for arm $a$ increases.
3. Elimination: In each phase $p$, for each arm $a$ in the active set $A_p$, the algorithm compares its UCB with other arms' LCB. If there exists an arm $a'$ such that: $UCB_t(a) < LCB_t(a')$, then arm $a$ is considered non-optimal and can be eliminated, resulting in a new active set $A_{p+1}$.
4. Selection: When making decisions, the algorithm only selects from the current active set $A_p$, ignoring eliminated arms. Arms in the active set have overlapping UCB and LCB, making them all potential optimal arms.

Example 2.3

Suppose there are 5 arms, and after initial exploration, we have the following empirical mean rewards:

• A: $\hat{\mu}_1$ = 0.3
• B: $\hat{\mu}_2$ = 0.5
• C: $\hat{\mu}_3$ = 0.4
• D: $\hat{\mu}_4$ = 0.2
• E: $\hat{\mu}_5$ = 0.6

For simplicity, assume the confidence interval radius $\beta=0.1$.

The initial active set is $A1 = \{1,2,3,4,5\}$.

At the end of Phase 1:

• A: $[0.2, 0.4]$
• B: $[0.4, 0.6]$
• C: $[0.3, 0.5]$
• D: $[0.1, 0.3]$
• E: $[0.5, 0.7]$

Comparing UCB and LCB, we can eliminate D because: $UCB_D = 0.3 < LCB_B = 0.4$

Thus, the active set for Phase 2 becomes $A2 = \{A, B, C, E\}$.

Chapter 3: UCB (Upper Confidence Bound) Algorithm Detailed Analysis

Let's first recall an important lemma:

For any $\delta \in (0,1]$, with confidence at least $1-\delta$, for all arms $a$ and time $t$:

$ |\hat{\mu}_t(a)-\mu(a)| \leq \beta_t(a) := \sqrt{\frac{\log(2KT/\delta)}{2N_t(a)}} $

Here $\hat{\mu}_t(a)$ is the mean estimate for arm $a$ at time $t$, and $N_t(a)$ is the number of times arm $a$ has been selected before time $t$.

The UCB algorithm is relatively mature and widely used for multi-armed bandit problems. It demonstrates a fundamental principle—maintaining an optimistic attitude when facing uncertainty.

Let's recall the definition of UCB:

UCB (Upper Confidence Bound): empirical mean reward, calculated as $\hat{\mu}_t(a) + \beta_t(a)$

Why is UCB a better algorithm compared to Successive Elimination, even though it only maintains the upper bound of rewards without considering the lower bound?

Since UCB consists of two parts, we can examine this question from two perspectives:

• $\hat{\mu}_t(a)$ is large: At time $t$, if arm $a$ has a large $\hat{\mu}_t(a)$, it means this arm has high rewards, which is clearly what we want.
• $\beta_t(a)$ is large: This means $N_t(a)$ is small, indicating we haven't tried this arm many times.

Obviously, in both cases, we have good reasons to select arm $a$.

Example 3.1

Suppose there are five arms, each representing a strategy. Each pull of an arm yields a reward: 1 (success) or 0 (failure).

Initially, each arm has been tried once, yielding the following rewards:

• A: 1
• B: 1
• C: 0
• D: 0
• E: 1

After the first round of trials, the total number of attempts is 5. Now let's select an arm for the 6th attempt:

• A: UCB(A) = 1 + $\sqrt{2\ln(5)/1}$ = 1 + 1.79 = 2.79
• B: UCB(B) = 1 + $\sqrt{2\ln(5)/1}$ = 2.79
• C: UCB(C) = 0 + $\sqrt{2\ln(5)/1}$ = 1.79
• D: UCB(D) = 0 + $\sqrt{2\ln(5)/1}$ = 1.79
• E: UCB(E) = 1 + $\sqrt{2\ln(5)/1}$ = 2.79

Algorithm Analysis

Initial Range of R(T)

For each round $t$, define: $r_t = \mu(a^*) - \mu(a_t)$.

Therefore: $R(T) = \sum_{t=1}^{T} r_t$

As mentioned before, we define a good event $\epsilon$:

$ \epsilon := \left\{ \forall a, \forall t, | \hat\mu_t(a) - \mu(a)| \leq \beta_t(a) \right\} $

Under the good event, for $r_t$, we have:

$ r_t = \mu(a^* ) - \mu(a_t) = \mu(a^* ) - UCB_t(a^* ) + UCB_t(a^*) - UCB_t(a_t) + UCB_t(a_t) - \mu(a_t) \leq 2\beta_t(a_t) $

Let's break down the above equation into three parts:

1. First part: $\mu(a^* ) - UCB_t(a^* ) = \mu(a^* ) - \hat{\mu}_t(a) - \beta_t(a)$
   Based on the definition of good event, we know this part is less than or equal to 0
2. Second part: $UCB_t(a^*) - UCB_t(a_t)$
   According to the UCB algorithm, we know that we only select the arm with the highest UCB value in each round, meaning the UCB value of our selected $a_t$ is the highest among all arms, so this part is also less than or equal to 0
3. Third part: $UCB_t(a_t) - \mu(a_t)$
   Again, based on the definition of good event

Therefore, we get:

$ R(T) = \sum_{t=1}^{T} r_t \leq \sum_{t=1}^{T} 2\beta_t(a_t) \leq 2 \times \sum_{t=1}^{T} \sqrt { \frac{\log(2KT/\delta)}{2N_t(a_t)} } $

Rearranging the above equation by moving terms independent of $t$ outside the summation:

$ R(T) \leq \sqrt { \log(2KT/\delta)} \times c \times \sum_{t=1}^{T} \sqrt { \frac{1}{N_t(a_t)} } $

Proving the Sum is Bounded

First, we can split the sum into sums over different arms $a$:

$ \sum_{t=1}^T \sqrt{\frac{1}{N_t(a_t)}} = \sum_{a=1}^K \sum_{t: a_t=a} \sqrt{\frac{1}{N_t(a)}} $

Here $t:a_t=a$ represents the cases where arm $a$ is selected in round $t$.

Chapter 4: Lower Bound Analysis of Regret in Multi-Armed Bandit Problems

In the previous chapter, we introduced the application of the Upper Confidence Bound (UCB) algorithm in Multi-Armed Bandit problems and proved that it can achieve an $O(\sqrt{T})$ upper bound on regret.

A natural question is whether this $\sqrt{T}$ upper bound on regret is optimal? Are there other better algorithms that can achieve a lower order of regret bound than $\sqrt{T}$?

To answer this question, we need to approach from another direction—exploring the lower bound of regret in Multi-Armed Bandit problems.

If we can prove that the lower bound of regret for any algorithm is $\sqrt{T}$, then we can conclude that the UCB algorithm is optimal, and no further improvement can be achieved by designing new algorithms.

Problem Formalization

Let $Alg$ represent the set of all possible Bandit algorithms, and $P$ represent the set of problem instances.

For any algorithm $A \in Alg$, the expected regret over $T$ rounds on problem instance $P$ is represented as $E_A[\bar{R_T}(A,P)]$. We define the expected regret of any algorithm in the worst case as:

$ R^* = \min_{A \in Alg} \max_P E_A[\bar{R_T}(A,P)] $

In other words, we want to find an algorithm A that minimizes the regret in the worst possible problem instance P.

$R^*$ is the regret that can be achieved by the optimal algorithm found in $Alg$ in the worst case.

That is, our goal is to prove that the lower bound of $R^*$ is $\Omega(\sqrt{T})$.

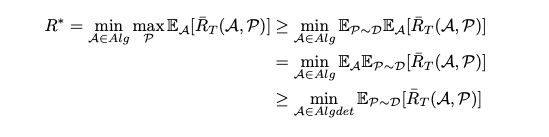
Proof Strategy

To prove the lower bound of regret, we will apply the minimax principle:

That is, if we can construct a problem distribution D such that any deterministic algorithm A has a lower bound on expected regret under this distribution, then we can deduce the lower bound of regret in the worst case.

Therefore, our technical approach is:

1. Construct a "difficult" problem distribution D
2. Prove that under distribution D, any deterministic algorithm A has an $\Omega(\sqrt{T})$ lower bound on expected regret

Simple Proof for Two-Armed Case

Let's first prove the simple case with only two arms, then summarize the pattern and extend it to multiple arms:

We select one arm as the optimal arm with average reward of $1/2+\epsilon$, while the other has $1/2$. To distinguish between these two arms, we need to make the estimation error less than $\epsilon$.

We know from Hoeffding's inequality that the error decays at a rate of $1/\sqrt{n}$.

Therefore, the sample size $n$ must satisfy $1/\sqrt{n} < \epsilon$, meaning we require the error decay rate to be less than $\epsilon$.

If the estimation error is greater than or equal to $\epsilon$, we might incorrectly select the suboptimal arm, as we cannot determine whether the observed difference is due to the true difference in expected rewards or due to estimation error.

Thus, we can easily derive $n > \frac{1}{\epsilon^2}$

This means one must pull the suboptimal arm at least $\frac{1}{\epsilon^2}$ times.

Each selection of the suboptimal arm produces at least $\epsilon$ regret.

Therefore, the total regret is at least $\frac{1}{\epsilon^2} \times \epsilon = \frac{1}{\epsilon}$.

If we choose $\epsilon = \frac{1}{\sqrt{T}}$, then the regret will be at least $\Omega(\sqrt{T})$.

(Note: If $\epsilon$ is chosen too small, the required number of pulls would exceed T, which would be meaningless in practical scenarios.)

References

1. ECE7995: Online Decision Making [https://sites.google.com/view/ece7995/home] Lecture 13-15
2. Introduction to Multi-Armed Bandits (II) Stochastic Bandits [https://blog.csdn.net/weixin_39059031/article/details/105690221]
3. Reinforcement Learning Theory Foundations 4.1 Bandit Introduction and Regret Decomposition Lemma [https://www.bilibili.com/video/BV18F411e7QR/]