Reinforcement learning is a significant branch in the fields of artificial intelligence and machine learning. Its goal is to enable an agent to learn the optimal policy through interactions with the environment.
The content of these notes is sourced from Professor Shiyu Zhao from the Intelligent Unmanned Systems Laboratory at Westlake University, specifically from the reinforcement learning course: Mathematical Foundations of Reinforcement Learning. Interested students can refer to the professor's course materials.
1. Grid World Example
To gain a more intuitive understanding of the basic concepts of reinforcement learning, let's first look at a simple grid world example. Imagine a robot (agent) moving within a 3x3 grid world, where some cells are forbidden, and there is a target cell. The robot's task is to find the optimal path from any starting position to the target cell while avoiding forbidden areas and unnecessary detours.
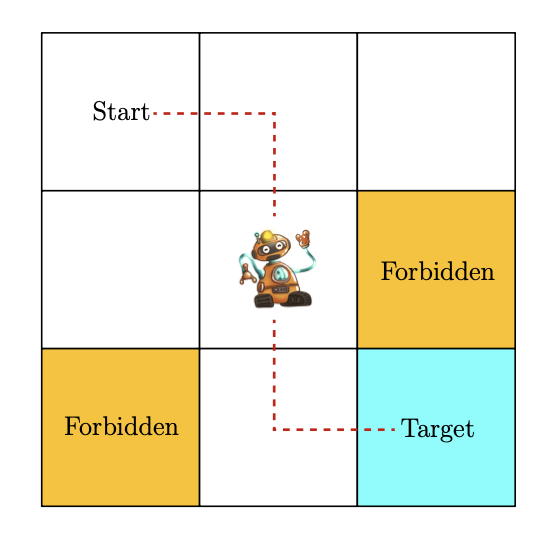
2. State and Action
A state describes the position or condition of the agent within the environment. In the grid world, a state corresponds to the robot's current cell position. We can represent these 9 states as $s_1, s_2, \ldots, s_9$. The set of all possible states forms the state space $S = \{s_1, \ldots, s_9\}$.
An action is a behavior that the agent can take. In this example, the robot has five possible actions in each state: move up, move right, move down, move left, and stay still. We represent these five actions as $a_1, a_2, \ldots, a_5$. The set of all possible actions forms the action space $A = \{a_1, \ldots, a_5\}$.
It is important to note that different states may have different action spaces. For instance, in the boundary cell $s_1$, moving up ($a_1$) or left ($a_4$) would result in a collision with a wall. Therefore, the action space for $s_1$ might only include $\{a_2, a_3, a_5\}$. However, to simplify the problem, we usually assume that all states share the same action space.
3. State Transition
When the agent performs an action in a particular state, it transitions from the current state to the next state. This process is known as state transition. For example, if the robot performs the action of moving right ($a_2$) in state $s_1$, it transitions to state $s_2$. We can represent this as: $s_1 \xrightarrow{a_2} s_2$.
State transitions can be described using conditional probabilities. For instance, $p(s_2|s_1, a_2) = 1$ indicates that performing action $a_2$ in state $s_1$ will result in a transition to state $s_2$ with probability 1. In a deterministic environment, state transitions are certain, but in a stochastic environment, state transitions may be probabilistic.
4. Policy
A policy is a method by which the agent selects actions in each state. Intuitively, we can imagine a policy as a series of arrows indicating which action the agent should take in each state.
Mathematically, a policy can be represented by the conditional probability $\pi(a|s)$, which denotes the probability of choosing action $a$ in state $s$. For example, $\pi(a_2|s_1) = 1$ means that in state $s_1$, action $a_2$ will always be chosen.
A policy can be deterministic, meaning it selects a specific action in each state, or stochastic, meaning it may choose different actions with certain probabilities in a given state.
5. Reward
Reward is one of the most distinctive concepts in reinforcement learning. After performing an action, the agent receives a reward signal $r$ from the environment. This reward is a function of the state $s$ and the action $a$, denoted as $r(s,a)$. Rewards can be positive, negative, or zero.
In the grid world example, we can design the rewards as follows:
- If the agent attempts to move out of bounds, the reward is -1 ($r_{boundary} = -1$)
- If the agent attempts to enter a forbidden area, the reward is -1 ($r_{forbidden} = -1$)
- If the agent reaches the target state, the reward is +1 ($r_{target} = +1$)
- In all other cases, the reward is 0 ($r_{other} = 0$)
The reward mechanism can be seen as the interface between humans and the agent, allowing us to guide the agent to act in the desired manner. Designing an appropriate reward function is a critical step in reinforcement learning. Although it can sometimes be challenging, it is usually simpler than solving the problem directly.
6. Trajectory, Return, and Episode
A trajectory is a sequence of states, actions, and rewards formed during the agent's interaction with the environment. For example, following a certain policy, an agent might form the following trajectory:
$$ s_1 \xrightarrow{a_2,r=0} s_2 \xrightarrow{a_3,r=0} s_5 \xrightarrow{a_3,r=0} s_8 \xrightarrow{a_2,r=1} s_9 $$
Return is the sum of all rewards collected along the trajectory. For the above trajectory, the return is $0 + 0 + 0 + 1 = 1$. Return is also referred to as total reward or cumulative reward.
We can use return to evaluate the quality of a policy. A higher return indicates a better policy. However, it is important to note that return includes both immediate and future rewards. Therefore, when making decisions, we should not only consider immediate rewards but also the long-term cumulative return.
For infinitely long trajectories, we introduce the concept of discounted return:
$$ \text{discounted return} = 0 + \gamma \cdot 0 + \gamma^2 \cdot 0 + \gamma^3 \cdot 1 + \gamma^4 \cdot 1 + \gamma^5 \cdot 1 + \ldots $$
where $\gamma \in (0,1)$ is the discount factor. Introducing the discount factor has two benefits: first, it prevents the return from diverging in infinitely long trajectories; second, by adjusting $\gamma$, we can control the agent's emphasis on immediate versus future rewards.
An episode is a complete trajectory from an initial state to a terminal state. Tasks with terminal states are called episodic tasks, while tasks without terminal states are called continuing tasks.
7. Markov Decision Processes (MDPs)
A Markov Decision Process is a general framework for describing reinforcement learning problems. An MDP consists of the following key elements:
- State space $S$
- Action space $A(s)$, where each state $s \in S$ has a corresponding set of actions
- Reward set $R(s,a)$, where each state-action pair $(s,a)$ has an associated reward
- State transition probability $p(s'|s,a)$, representing the probability of transitioning to state $s'$ after taking action $a$ in state $s$
- Reward probability $p(r|s,a)$, representing the probability of receiving reward $r$ after taking action $a$ in state $s$
- Policy $\pi(a|s)$, representing the probability of choosing action $a$ in state $s$
An important characteristic of an MDP is the Markov property, which states that the next state and reward depend only on the current state and action, not on the previous history:
$$ p(s_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, \ldots, s_0, a_0) = p(s_{t+1}|s_t, a_t) $$
$$ p(r_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, \ldots, s_0, a_0) = p(r_{t+1}|s_t, a_t) $$
This property is crucial for deriving the fundamental equations of reinforcement learning, such as the Bellman equation.
8. Additional Notes
- Design of Rewards: As mentioned in the PDF, the design of rewards can be relative. For example, adding a constant to all reward values does not change the optimal policy.
- Relationship Between Rewards and Next State: Although we typically represent rewards as $r(s,a)$, rewards may also depend on the next state $s'$. We can convert this dependency to depend only on $s$ and $a$ by using: $$ p(r|s,a) = \sum_{s'} p(r|s,a,s') p(s'|s,a) $$