In reinforcement learning, evaluating the effectiveness of a policy is crucial. This chapter will introduce two core concepts: state value and the Bellman equation, which are fundamental tools for policy evaluation. State value is defined as the average reward that an agent can obtain while following a given policy. The higher the state value, the better the corresponding policy. Therefore, state values can serve as metrics for evaluating policy quality.
However, merely understanding the importance of state values is insufficient; we also need to know how to analyze them. This is where the Bellman equation comes into play. The Bellman equation is a vital tool for analyzing state values, describing the relationships between all state values. Through solving the Bellman equation, we can obtain state values. This process is known as policy evaluation, a fundamental concept in reinforcement learning.
This chapter will delve into these concepts, starting with simple examples and gradually introducing more complex mathematical expressions. We will learn how to construct Bellman equations, how to solve them, and how to interpret the results. Additionally, this chapter will introduce another important concept: action value, and explore its relationship with state value.
1. Why Focus on Returns?
Let's first look at a simple example to illustrate the importance of returns:
Consider three different policies:
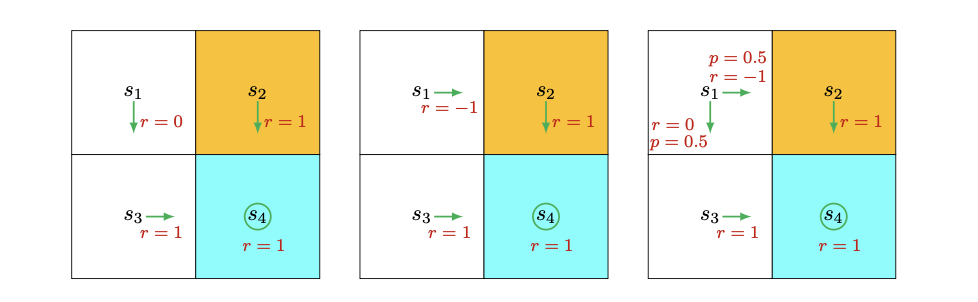
Intuitively, the left policy is the best because an agent starting from s1 can avoid the forbidden area. The middle policy appears worst as it leads directly into the forbidden area from s1. The right policy falls between these two, with a 0.5 probability of entering the forbidden area.
How can we mathematically describe these intuitive judgments? The answer lies in the concept of returns.
Assuming the agent starts from s1, with a discount rate $\gamma$ $(0 < \gamma < 1)$:
- Following the first policy, the trajectory is $s_1 \rightarrow s_3 \rightarrow s_4 \rightarrow s_4 ...$, with discounted return:
$ return_1 = 0 + \gamma1 + \gamma^2 1 + ... = \frac{\gamma}{1-\gamma} $
- Following the second policy, the trajectory is $s_1 \rightarrow s_2 \rightarrow s_4 \rightarrow s_4 ...$, with discounted return:
$ return_2 = -1 + \gamma1 + \gamma^2 1 + ... = -1 + \frac{\gamma}{1-\gamma} $
- Following the third policy, there are two possible trajectories, each with probability 0.5:
$s_1 \rightarrow s_3 \rightarrow s_4 \rightarrow s_4 ...$
$s_1 \rightarrow s_2 \rightarrow s_4 \rightarrow s_4 ...$
The average discounted return is:
$ return_3 = 0.5(-1 + \frac{\gamma}{1-\gamma}) + 0.5(\frac{\gamma}{1-\gamma}) = -0.5 + \frac{\gamma}{1-\gamma} $
Comparing the returns of the three policies, we can find:
$ return_1 > return_3 > return_2 $
This mathematical conclusion aligns with our earlier intuitive judgment: the first policy is best because it can avoid the forbidden area; the second policy is worst because it leads directly into the forbidden area.
This example shows that returns can be used to evaluate the quality of policies: higher returns indicate better policies.
2. How to Calculate Returns?
Since returns are so important, how do we calculate them? There are two methods:
2.1 Direct Calculation by Definition
Returns equal the discounted sum of all rewards collected along the trajectory. Consider the following example:
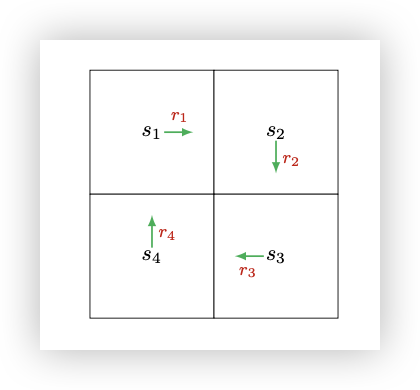
If we let $v_i$ represent the return starting from $s_i$, then:
$ \begin{align*} v_1 &= r_1 + \gamma r_2 + \gamma^2 r_3 + ... \\ v_2 &= r_2 + \gamma r_3 + \gamma^2 r_4 + ... \\ v_3 &= r_3 + \gamma r_4 + \gamma^2 r_1 + ... \\ v_4 &= r_4 + \gamma r_1 + \gamma^2 r_2 + ... \end{align*} $
2.2 Bootstrap Method
Observing the above expressions, we can rewrite them as:
$ \begin{align*} v_1 &= r_1 + \gamma(r_2 + \gamma r_3 + ...) = r_1 + \gamma v_2 \\ v_2 &= r_2 + \gamma(r_3 + \gamma r_4 + ...) = r_2 + \gamma v_3 \\ v_3 &= r_3 + \gamma(r_4 + \gamma r_1 + ...) = r_3 + \gamma v_4 \\ v_4 &= r_4 + \gamma(r_1 + \gamma r_2 + ...) = r_4 + \gamma v_1 \end{align*} $
These equations show that return values are interdependent, reflecting the bootstrap method's idea: obtaining values from itself.
From a mathematical perspective, these equations can be rewritten as a linear matrix-vector equation:
$ \begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{bmatrix} = \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{bmatrix} + \gamma \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{bmatrix} $
Concisely expressed as:
$ v = r + \gamma P v $
where $v$ can be obtained by solving: $v = (I - \gamma P)^{-1} r$.
This simple example demonstrates the core idea of the Bellman equation: the return obtained starting from one state depends on the returns obtained starting from other states.
3. State Value
Although returns can be used to evaluate policies, they are not suitable in random systems because starting from one state can lead to different returns. To address this issue, we introduce the concept of state value.
First, let's introduce some necessary notation. Consider a series of time steps $t = 0, 1, 2, ...$. At time $t$, the agent is in state $S_t$, takes action $A_t$ according to policy $\pi$. The next state is $S_{t+1}$, and the immediate reward is $R_{t+1}$. This process can be concisely represented as:
$ S_t \xrightarrow{A_t} S_{t+1}, R_{t+1} $
Note that $S_t$, $S_{t+1}$, $A_t$, $R_{t+1}$ are all random variables.
Starting from $t$, we can obtain a state-action-reward trajectory:
$ S_t \xrightarrow{A_t} S_{t+1}, R_{t+1} \xrightarrow{A_{t+1}} S_{t+2}, R_{t+2} \xrightarrow{A_{t+2}} S_{t+3}, R_{t+3} ... $
By definition, the discounted return along this trajectory is:
$ G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... $
where $\gamma \in (0,1)$ is the discount rate. Note that $G_t$ is a random variable because $R_{t+1}, R_{t+2}, ...$ are all random variables.
Since $G_t$ is a random variable, we can calculate its expected value:
$ v_\pi(s) \doteq E[G_t|S_t = s] $
Here, $v_\pi(s)$ is called the state value function, or simply the state value of state $s$.
Regarding state values, there are several important points:
- $v_\pi(s)$ depends on $s$. This is because its definition is a conditional expectation, conditioned on the agent starting from $S_t = s$.
- $v_\pi(s)$ depends on $\pi$. This is because the trajectory is generated by following policy $\pi$. Different policies may lead to different state values.
- $v_\pi(s)$ does not depend on $t$. When the agent moves in the state space, $t$ represents the current time step. Once the policy is given, the value of $v_\pi(s)$ is determined.
4. Bellman Equation
Since state values are so important, how do we calculate them? The answer lies in the Bellman equation, which is a mathematical tool for analyzing state values. In short, the Bellman equation is a set of linear equations describing the relationships between all state values.
Let's now derive the Bellman equation. First, notice that $G_t$ can be rewritten as:
$ \begin{align*} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... \\ &= R_{t+1} + \gamma(R_{t+2} + \gamma R_{t+3} + ...) \\ &= R_{t+1} + \gamma G_{t+1} \end{align*} $
where $G_{t+1} = R_{t+2} + \gamma R_{t+3} + ...$. This equation establishes the relationship between $G_t$ and $G_{t+1}$. Then, the state value can be written as:
$ \begin{align*} v_\pi(s) &= E[G_t|S_t = s] \\ &= E[R_{t+1} + \gamma G_{t+1}|S_t = s] \\ &= E[R_{t+1}|S_t = s] + \gamma E[G_{t+1}|S_t = s] \end{align*} $
The two terms in the equation can be analyzed separately:
-
The first term $E[R_{t+1}|S_t = s]$ is the expected immediate reward. Using the law of total expectation, it can be calculated as:
$ E[R_{t+1}|S_t = s] = \sum_{a\in A} \pi(a|s) E[R_{t+1}|S_t = s, A_t = a] = \sum_{a\in A} \pi(a|s) \sum_{r\in R} p(r|s, a)r $
Here, $A$ and $R$ are the sets of possible actions and rewards respectively.
-
The second term $E[G_{t+1}|S_t = s]$ is the expected future rewards. It can be calculated as:
$ \begin{align*} E[G_{t+1}|S_t = s] &= \sum_{s'\in S} E[G_{t+1}|S_t = s, S_{t+1} = s'] p(s'|s) \\ &= \sum_{s'\in S} E[G_{t+1}|S_{t+1} = s'] p(s'|s) \quad \text{(due to Markov property)} \\ &= \sum_{s'\in S} v_\pi(s') p(s'|s) \\ &= \sum_{s'\in S} v_\pi(s') \sum_{a\in A} p(s'|s, a)\pi(a|s) \end{align*} $
Substituting these terms back into the original equation, we get the Bellman equation:
$ v_\pi(s) = \sum_{a\in A} \pi(a|s) \left[\sum_{r\in R} p(r|s, a)r + \gamma \sum_{s'\in S} p(s'|s, a)v_\pi(s')\right], \quad \forall s \in S $
This equation looks complex, but it has a clear structure. Here are some explanations:
- $v_\pi(s)$ and $v_\pi(s')$ are the unknown state values to be computed. Beginners might be confused about how to calculate the unknown $v_\pi(s)$ since it depends on another unknown $v_\pi(s')$. It's important to note that the Bellman equation refers to a set of linear equations for all states, not a single equation.
- $\pi(a|s)$ is the given policy. Since state values can be used to evaluate policies, solving state values from the Bellman equation is a policy evaluation process, which is an important process in many reinforcement learning algorithms.
- $p(r|s, a)$ and $p(s'|s, a)$ represent the system model.
8. Summary
The most important concept introduced in this chapter is state value. Mathematically, state value is the expected return that an agent can obtain starting from a state. Values of different states are interconnected, meaning that the value of state $s$ depends on the values of some other states, which in turn might depend on the value of state $s$ itself. This phenomenon might be the most confusing part of this chapter for beginners. It is related to an important concept called "bootstrapping," which involves calculating something from itself. Although bootstrapping might be confusing intuitively, it becomes clear if we examine the matrix-vector form of the Bellman equation. Specifically, the Bellman equation is a set of linear equations describing the relationships between all state values.
Since state values can be used to evaluate policy quality, the process of solving state values from the Bellman equation is called policy evaluation. As we will see later in this book, policy evaluation is an important step in many reinforcement learning algorithms.
Another important concept, action value, was introduced to describe the value of taking an action in a state. As we will see later in this book, action values play a more direct role than state values when we try to find optimal policies.
Finally, the Bellman equation is not limited to the field of reinforcement learning. Instead, it exists widely in many fields such as control theory and operations research. In different fields, the Bellman equation might have different expressions. In this book, the Bellman equation is studied under discrete Markov decision processes.
By understanding these fundamental concepts and tools, we have laid a solid foundation for the in-depth study of reinforcement learning. In the following chapters, we will see how to utilize these concepts to develop and analyze various reinforcement learning algorithms.
References
- Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.
- Bertsekas, D. P. (2019). Reinforcement learning and optimal control. Athena Scientific.
- Powell, W. B. (2011). Approximate Dynamic Programming: Solving the curses of dimensionality (Vol. 703). John Wiley & Sons.